KNN vs. les Sup
1. Fonctions auxiliaires
1.1. Chargement des données.
def chargement(chemin): fichier = open(chemin, 'r') donnees = [] etiquettes = [] lignes = fichier.readlines() for li in lignes: l_li = li.split(',') ident, note = int(l_li[0]), int(l_li[1]) vecteur = [ float(l_li[i]) for i in range(2, len(l_li)) ] donnees.append(vecteur) etiquettes.append(note) fichier.close() return donnees, etiquettes
1.2. Distances
def distance(v1,v2) : somme = 0 for i in range(len(v1)) : somme += (v1[i] - v2[i]) ** 2 return somme ** 0.5
2. KNN
2.1. Plus proche
def plus_proches(k, donnees, vecteur): kpp = [ (None, float("inf")) ] * k for i in range(len(donnees)): d = distance(donnees[i], vecteur) if d < kpp[k-1][1]: j = k-1 while j > 0 and kpp[j-1][1] > d: kpp[j] = kpp[j-1] j -= 1 kpp[j] = (i, d) return kpp
2.2. Stratégie majoritaire
def majo(kpp, etiquettes): # Calcul du nombre d'occurrences d = {} for i,dist in kpp: e = etiquettes[i] if e in d: d[e] += 1 else: d[e] = 1 # Calcul de la clé du maximum m = -float("inf") e = None for k, v in d.items(): if v > m: m = v e = k return e
2.3. Stratégie moyenne
def moyenne(kpp, etiquettes): somme = 0 for i,dist in kpp: somme += etiquettes[i] return round(somme / len(kpp))
2.4. Stratégie moyenne pondérée
def moyenne_ponderee(kpp, etiquettes): somme = 0 sdist = 0 for i,dist in kpp: if dist == 0: return etiquettes[i] somme += etiquettes[i] * (1 / dist) sdist += (1 / dist) return round(somme / sdist)
3. Analyse des résultats
3.1. Matrice de confusion
def confusion(k, strategie, d_tr, l_tr, d_test, l_test): matrice = [ [0] * 21 for i in range(21) ] for i in range(len(d_test)): res_ia = knn(k, strategie, d_tr, l_tr, d_test[i]) res_reel = l_test[i] matrice[res_reel][res_ia] += 1 return matrice
3.2. Taux d’erreur empirique
def taux_erreur_empirique(matrice): nerr, ntot = 0, 0 n = len(matrice) for i in range(n): for j in range(n): if i != j : nerr += matrice[i][j] ntot += matrice[i][j] return (nerr / ntot)
3.3. Erreur quadratique moyenne
def erreur_quad_moyenne(matrice): n = len(matrice) erreurs = 0 total = 0 for i in range(n): for j in range(n): total += matrice[i][j] if i != j: erreurs += matrice[i][j] * (i-j)**2 return erreurs / total
3.4. Statistiques
strategies = [ majo, moyenne, moyenne_ponderee ] res = [] for strat in strategies: matrices = [ confusion(k, strat, data_tr, labels_tr, data_test, labels_test) for k in range(1,30) ] taux = [ taux_erreur_empirique(m) for m in matrices ] errs = [ erreur_quad_moyenne(m) for m in matrices ] res.append((matrices, taux, errs))
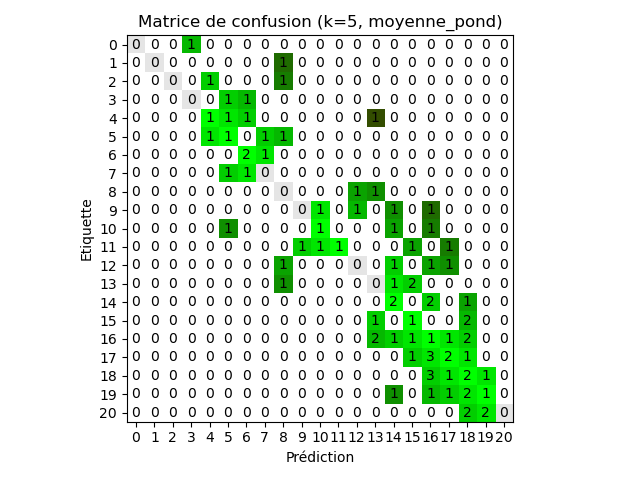
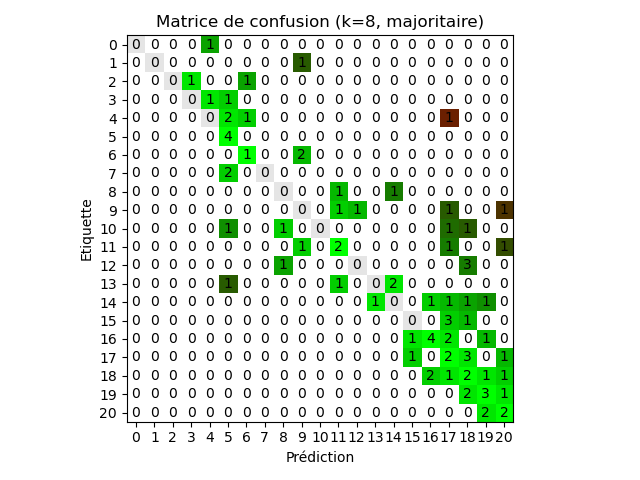
On trouve avec l’échantillon donné, un meilleur taux d’erreur empirique pour la
stratégie du majorant et une meilleure erreur
quadratique moyenne avec la stratégie de
moyenne pondérée (k = 8 et k = 5 respectivement)
4. Sélection préalables des données
4.1. Tri à bulles
def tri_bulles(l): for i in range(1, len(l)): for j in range(len(l)-i): if l[j] > l[j+1]: l[j], l[j+1] = l[j+1], l[j]
4.2. Sélection aléatoire
L’intérêt d’avoir trié les indices est de pouvoir comparer un indice de l
uniquement au premier élément non traité de la sélection d’indices.
import random as rd def selection(l, p): indices = [ i for i in range(len(l)) ] indices_select = rd.sample(indices, (len(l)*p // 100)) tri_bulles(indices_select) select = [] nonselect = [] j = 0 # indice du premier élément non ajouté à select # Invariants : # 1. select contient les éléments de indices_select[:j] # 2. non select contient les élements < i qui ne sont pas dans # indices_select[:j] # 3. i <= indices_select[j] # 4. i est plus grand strictement que tous les éléments de select for i in range(len(l)): if j < len(indices_select) and i == indices_select[j]: select.append(l[i]) j += 1 else: # Valide ici si i != j, alors i < j (3.) # et (4. + 1.) i not in indices_select. nonselect.append(l[i]) return select, nonselect
4.3. GROUP BY label
C’est comme un décompte du nombre d’occurrences mais on ajoute dans une liste au lieu de compter.
def groupby(donnees, etiquettes): d = {} for i in range(len(etiquettes)): if etiquettes[i] in d: d[etiquettes[i]].append(i) else: d[etiquettes[i]] = [i] return d
4.4. Échantillons
def echantillons(donnees, etiquettes): par_e = groupby(donnees, etiquettes) d_tr = [] l_tr = [] d_test = [] l_test = [] for e, d in par_e.items(): entr, test = selection(d, 80) d_tr += [donnees[i] for i in entr] l_tr += [e]*len(entr) d_test += [donnees[i] for i in test] l_test += [e] * len(test) return d_tr, l_tr, d_test, l_test
4.5. Sauvegarde
def sauvegarde(chemin, donnees, etiquettes): fentr = open(chemin, 'w') for i in range(len(donnees)): fentr.write(','.join([str(i),str(etiquettes[i])] + [str(x) for x in donnees[i]]) + '\n') data, labels = chargement('data.csv') data_tr, labels_tr, data_test, labels_test = echantillons(data, labels) sauvegarde('my_data_training.csv', data_tr, labels_tr) sauvegarde('my_data_test.csv', data_test, labels_test)